A stochastic bandit with $K$ actions is completely determined by the distributions of rewards, $P_1,\dots,P_K$, of the respective actions. In particular, in round $t$, the distribution of the reward $X_t$ received by a learner choosing action $A_t\in [K]$ is $P_{A_t}$, regardless of the past rewards and actions. If one looks carefully at any “real-world” problem, let it be drug design, recommending items on the web, or anything else, we will soon find out that there are in fact no suitable distributions. First, it will be hard to argue that the reward is truly randomly generated and even if it was randomly generated, the rewards could be correlated over time. Taking account all these effects would make a stochastic model potentially quite complicated. An alternative is to take a pragmatic approach, where almost nothing is assumed about the mechanism that generates the rewards, while still keeping the objective of competing with the best action in hindsight. This leads to the so-called adversarial bandit model, the subject of this post. That we are still competing with the single best action in hindsight expresses the prior belief that the world is stationary, the assumption that we made quite explicit in the stochastic setting. Because a learning algorithm still competes with the best action in hindsight, as we shall see soon, learning is still possible in the sense that the regret can be kept sublinear. But, as we shall see, the algorithms need to be radically different than in the stochastic setting.
In the remainder of the post, we first introduce the formal framework of “adversarial bandits” and the appropriately adjusted concept of minimax regret. Next, we point out that adversarial bandits are at least as hard as stochastic bandits and as a result, immediately giving a lower bound on the minimax regret. The next question is whether there are algorithms that can meet the lower bound. Towards this goal we discuss the so-called Exp3 (read: “e-x-p 3”) algorithm and show a bound on its expected regret, which almost matches the lower bound, thus showing that, from a worst-case standpoint, adversarial bandits are effectively not harder than stochastic bandits. While having a small expected regret is great, Exp3 is randomizing and hence its regret will also be random. Could it be that the upper tail of the regret is much larger than its expectation? This question is investigated at the end of post, where we introduce Exp3-IX (Exp3 “with implicit exploration”), a variant of Exp3, which is shown to also enjoy a “small” regret with high probability (not only in expectation).
Adversarial bandits
An adversarial bandit environment $\nu$ is given by an arbitrary sequence of reward vectors $x_1,\dots,x_n\in [0,1]^K$. Given the environment $\nu = (x_1,\dots,x_n)\in [0,1]^{Kn}$, the model says that in round $t$ the reward of action $i\in [K]$ is just $x_{ti}$ (this is the $i$th entry in vector $x_t$). Note that we are using lower-case letters for the rewards. This is because the reward table is just a big table of numbers: the rewards are non-random. In fact, since arbitrary sequences are allowed, random rewards would not increase generality, hence we just work with deterministic rewards.
The interconnection of a policy $\pi$ and an environment $\nu = (x_1,\dots,x_n)\in [0,1]^{nK}$ works as follows: A policy $\pi$ interacting with an adversarial bandit environment $\nu$ chooses actions in a sequential fashion in $n$ rounds. In the first round, the policy chooses $A_1 \sim p_1(\cdot)$ possibly in a random fashion (hence, the upper case for $A_1$). As a result, the reward $X_1 = x_{1,A_1}$ is “sent back” to the policy. Note that $X_1$ is random since $A_1$ is random. More generally, in round $t\in [n]$, $A_t$ is chosen based on $A_1,X_1,\dots,A_{t-1},X_{t-1}$: $A_t \sim \pi_t(\cdot| A_1,X_1,\dots,A_{t-1},X_{t-1} )$. The reward incurred as a result is then $X_t = x_{t,A_t}$. This is repeated $n$ times, where $n$ may or may not be given a priori.
The goal is to design a policy $\pi$ that keeps the regret small no matter what rewards $\nu = (x_1,\dots,x_n)$ are assigned to the actions. Here, the regret (more precisely, expected regret) of a policy $\pi$ choosing $A_1,\dots,A_n$ while interacting with the environment $\nu = (x_1,\dots,x_n)$ is defined as
\begin{align*}
R_n(\pi,\nu) = \EE{\max_{i\in [K]} \sum_{t=1}^n x_{ti} – \sum_{t=1}^n x_{t,A_t}}\,.
\end{align*}
That is, performance is measured by the expected revenue lost when compared with the best action in hindsight. When $\pi$ and $\nu$ are clear from the context, we may just write $R_n$ in place of $R_n(\pi,\nu)$. Now, the quality of a policy is defined through its worst-case regret
\begin{align*}
R_n^*(\pi) = \sup_{\nu\in [0,1]^{nK}} R_n(\pi,\nu)\,.
\end{align*}
Similarly to the stochastic case, the main question is whether there exists policies $\pi$ such that the growth of $R_n^*(\pi)$ (as a function of $n$) is sublinear.
The problem is only interesting when $K>1$, which we assume from now on. Then, it is clear that unless $\pi$ is randomizing, its worst-case regret can be forced to be equal to $n$, which is in fact the largest possible value that the regret can take. Indeed, if $\pi$ is not randomizing, in every round $t$, we can use the past actions $a_1,\dots,a_{t-1}$ and rewards $x_{1,a_1},\dots,x_{t-1,a_{t-1}}$ to query $\pi$ for the next action. If we find that this is $a_t$, we set $x_{t,a_t} = 0$ and $x_{t,i}=1$ for all other $i\ne a_t$. This way, we obtain a sequence $\nu= (x_1,\dots,x_n)$ such that $R_n(\pi,\nu) = n$, as promised.
When $\pi$ randomizes, the above “second-guessing” strategy does not work anymore. As we shall see soon, randomization will indeed result in policies with good worst-case guarantees. Below, we will show that a regret that is almost as small as in the stochastic setting is possible. How is this possible? The key observation is that the goal of learning is modest: No environment can simultaneously generate large rewards for some actions and prevent a suitable learner to detect which action these large rewards are associated with. This is because the rewards are bounded and hence a large total reward means that the reward of the action has to be large often enough, which makes it relatively easy for a learner to identify the action with such large rewards. Before discussing how this can be achieved, we should first compare stochastic and adversarial models in a little more detail.
Relation between stochastic and adversarial bandits
We already noted that deterministic strategies will have linear worst-case regret. Thus, some strategies, including those that were seen to achieve a small worst-case regret for stochastic bandits, will give rise to large regret in the adversarial case. How about the other direction? Will an adversarial bandit strategy have small expected regret in the stochastic setting?
Note the subtle difference between the notions of regret in the stochastic and the adversarial cases: In the stochastic case, the total expected reward is compared to $\max_i \EE{ \sum_{t=1}^n X_{t,i}}$, the maximum expected reward, where $X_{t,i} \sim P_i$ iid, while in the adversarial case it is compared to the maximum reward. If the rewards are random themselves, the comparison is to the expectation of the maximum reward. Now, since $\EE{ \max_i \sum_{t=1}^n X_{t,i} } \ge \max_i \EE{ \sum_{t=1}^n X_{t,i}}$, we thus get that
\begin{align}
\EE{ \max_i \sum_{t=1}^n X_{t,i} – X_{t,A_t} } \ge \max_i \EE{ \sum_{t=1}^n X_{t,i} – X_{t,A_t} }\,.
\label{eq:stochadvregret}
\end{align}
(It is not hard to see that the distribution of $A_1,X_1,\dots,A_n,X_n$ with $X_t = X_{t,A_t}$ indeed satisfies the constraints that need to hold in the stochastic case, hence, the right hand-side is indeed the regret of the policy choosing $A_t$ in the environment $\nu = (P_i)_i$.)
The left-hand side of $\eqref{eq:stochadvregret}$ is the expected adversarial regret, while the right-hand side is the expected regret as defined for stochastic bandits. Thus, an algorithm designed to keep the adversarial regret small will achieve a small (worst-case) regret on stochastic problems, too. Reversely, the above inequality also implies that the worst-case regret for adversarial problems is lower bounded by the worst-case regret on stochastic problems. In particular, from our minimax lower bound for stochastic bandits, we get the following:
Theorem (Lower bound on worst-case adversarial regret): For any $n\ge K$, the minimax adversarial regret, $R_n^*= \inf_\pi \sup_{\nu\in [0,1]^{nK}} R_n(\pi,\nu)$, satisfies
\begin{align*}
R_n^* \ge c\sqrt{nK}\,,
\end{align*}
where $c>0$ is a universal constant.
The careful reader may notice that there is a problem with using the previous minimax lower bound developed for stochastic bandits in that this bound was developed for environments with Gaussian reward distributions. But Gaussian rewards are unbounded, and in the adversarial setting the rewards must lie in a bounded range. In fact, if in the adversarial setting the range of rewards is unbounded, all policies will suffer unbounded regret in the very first round! To fix the issue, one needs to re-prove the minimax lower bound for stochastic bandits using reward distributions that guarantee a bounded range for the rewards themselves. One possibility is to use Bernoulli rewards and this is indeed what is typically done. We leave the modification of the previous proof for the reader. One hint is in the proof instead of using zero means, one should use $0.5$, the reason being that the variance of Bernoulli variables decreases with their mean approaching zero, which makes learning about a mean close to zero easier. Keeping the means bounded away from zero (and one) will however allow our previous proof to go through with almost no changes.
Trading off exploration and exploitation with Exp3
The most standard algorithm for the adversarial bandit setting is the so-called Exp3 algorithm, where “Exp3” stands for “Exponential-weight algorithm for Exploration and Exploitation”. The meaning of the name will become clear once we discussed how Exp3 works.
In every round, the computation that Exp3 does has the following three steps:
- Sampling an action $A_t$ from a previously computed distribution $P_{ti}$;
- Estimating rewards for all the actions based on the observed reward $X_t$;
- Using the estimated rewards to update $P_{ti}$, $i\in [K]$.
Initially, in round one, $P_{1i}$ is set to the uniform distribution: $P_{1i} = 1/K$, $i\in [K]$.
Sampling from $P_{ti}$ means to select $A_t$ randomly such that given the past $A_1,X_1,\dots,A_{t-1},X_{t-1}$, $\Prob{A_t=i|A_1,X_1,\dots,A_{t-1},X_{t-1}}=P_{ti}$. This can be implemented for example by generating a sequence of independent random variables $U_1,\dots,U_n$ uniformly distributed over $[0,1)$ and then in round $t$ choosing $A_t$ to be the unique index $i$ such that $U_t$ falls into the interval $[\sum_{j=1}^{i-1} P_{tj}, \sum_{j=1}^i P_{tj})$. How rewards are estimated and how they are used to update $P_{ti}$ are the subject of next two section.
Reward estimation
We discuss reward estimation more generally as it is a useful building block of many algorithms. Thus, for some policy $\pi = (\pi_1,\dots,\pi_n)$, let $P_{ti} = \pi_t(i|A_1,X_1,\dots,A_{t-1},X_{t-1})$. (Note that $P_{ti}$ is also random as it depends on $A_1,X_1,\dots,A_{t-1},X_{t-1}$ which were random.) Assume that $P_{ti}>0$ almost surely (we will later see that Exp3 does satisfy this).
Perhaps surprisingly, reward estimation also benefits from randomization! How? Recall that $P_{ti} = \Prob{A_t = i| A_1,X_1,\dots,A_{t-1},X_{t-1}}$. Then, after $X_t$ is observed, we can use the so-called (vanilla) importance sampling estimator:
\begin{align}
\hat{X}_{ti} = \frac{\one{A_t=i}}{P_{ti}} \,X_t\,.
\label{eq:impestimate}
\end{align}
Note that $\hat{X}_{ti}\in \R$ is random (it depends on $A_t,P_t,X_t$, and all these are random). Is $\hat X_{ti}$ a “good” estimate of $x_{ti}$? A simple way to get a first impression of this is to calculate the mean and variance of $\hat X_{ti}$. Is the mean of $\hat{X}_{ti}$ close to $x_{ti}$? Does $\hat{X}_{ti}$ have a small variance? To study these, let us introduce the conditional expectation operator $\Et{\cdot}$: $\Et{Z} \doteq \EE{Z|A_1,X_1,\dots,A_{t-1},X_{t-1} }$. As far as the mean is concerned, we have
\begin{align}
\Et{ \hat{X}_{ti} } = x_{ti}\,,
\label{eq:unbiasedness}
\end{align}
i.e., $\hat{X}_{ti}$ is an unbiased estimate of $x_{ti}$. While it is not hard to see why $\eqref{eq:unbiasedness}$ holds, we include the detailed argument as some of the notation will be useful later. In particular, writing $A_{ti} \doteq \one{A_t=i}$, we have $X_t A_{ti} = x_{t,i} A_{ti}$ and thus,
\begin{align*}
\hat{X}_{ti} = \frac{A_{ti}}{P_{ti}} \,x_{ti}\,.
\end{align*}
Now, $\Et{A_{ti}} = P_{ti}$ (thus $A_{ti}$ is the “random $P_{ti}$”) and since $P_{ti}$ is a function of $A_1,X_1,\dots,A_{t-1},X_{t-1}$, we get
\begin{align*}
\Et{ \hat{X}_{ti} }
& =
\Et{ \frac{A_{ti}}{P_{ti}} \,x_{ti} }
=
\frac{x_{ti}}{P_{ti}} \, \Et{ A_{ti} }
=
\frac{x_{ti}}{P_{ti}} \, P_{ti} = x_{ti}\,,
\end{align*}
proving $\eqref{eq:unbiasedness}$. (Of course, $\eqref{eq:unbiasedness}$ also implies that $\EE{\hat X_{ti}}=x_{ti}$.) Let us now discuss the variance of $\hat X_{ti}$. Similarly to the mean, we will consider the conditional variance $\Vt{\hat X_{ti}}$ of $\hat X_{ti}$, where $\Vt{\cdot}$ is defined by $\Vt{U} \doteq \Et{ (U-\Et{U})^2 }.$ In particular, $\Vt{\hat X_{ti}}$ is the variance of the $\hat X_{ti}$ given the past, i.e., the variance due to the randomness of $A_t$ alone, disregarding the randomness of the history. The conditional variance is more meaningful than the full variance as the estimator itself has absolutely no effect on what happened in the past! Why would we want then to account for the variations due to the randomness of the history when discussing the quality of the estimator?
Hoping that the reader is convinced that it is the conditional variance that one should care of, let us see how big this quantity can be. As is well known, for $U$ random, $\Var(U) = \EE{U^2} – \EE{U}^2$. The same (trivially) holds for $\Vt{\cdot}.$ Hence, knowing that the estimate is unbiased, we see that we need to compute the second moment of $\hat X_{ti}$ only to get the conditional variance. Since $\hat{X}_{ti}^2 = \frac{A_{ti}}{P_{ti}^2} \,x_{ti}^2$, we have $\Et{ \hat{X}_{ti}^2 }=\frac{x_{ti}^2}{P_{ti}}$ and thus,
\begin{align}
\Vt{\hat{X}_{ti}} = x_{ti}^2 \frac{1-P_{ti}}{P_{ti}}\,.
\label{eq:vtimp}
\end{align}
In particular, we see that this can be quite large if $P_{ti}$ is small. We shall later see to what extent this can cause trouble.
While the estimate $\eqref{eq:impestimate}$ is perhaps the simplest one, this is not the only possibility. One possible alternative is to use
\begin{align}
\hat X_{ti} = 1- \frac{\one{A_t=i}}{P_{ti}}\,(1-X_t)\,.
\label{eq:lossestimate}
\end{align}
It is not hard to see that we still have $\Et{\hat X_{ti}} = x_{ti}$. Introducing $y_{ti} = 1-x_{ti}$, $Y_t = 1-X_t$, $\hat Y_{ti} = 1-\hat X_{ti}$, we can also see that the above formula can be written as
\begin{align*}
\hat Y_{ti} = \frac{\one{A_t=i}}{P_{ti}}\,Y_t\,.
\end{align*}
This is in fact the same formula as $\eqref{eq:impestimate}$ except that $X_t$ has been replaced by $Y_t$! Since $y_{ti}$, $Y_t$ and $\hat{Y}_{ti}$ have the natural interpretation of losses, we may notice that if we set up the framework with losses, this would have been the estimator that would have first come to mind. Hence, the estimator is called the loss-based importance sampling estimator. Unsurprisingly, the conditional variance of this estimator is also very similar to that of the previous one:
\begin{align*}
\Vt{\hat X_{ti}} = \Vt{\hat Y_{ti}} = y_{ti}^2 \frac{1-P_{ti}}{P_{ti}}\,.
\end{align*}
Since we expect $P_{ti}$ to be large for “good” actions (actions with large rewards, or small losses), based on this expression we see that the second estimator has smaller variance for “better” actions, while the first estimator has smaller variance for “poor” actions (actions with small rewards). Thus, the second estimator is more accurate for good actions, while the first is more accurate for bad actions. At this stage, one could be suspicious about the role of “zero” in all this argument. Can we change the estimator (either one of them) so that it is more accurate for actions whose reward is close to some specific value $v$? Of course! Just change the estimator so that $v$ is subtracted from the observed reward (or loss), then use the importance sampling formula, and then add back $v$.
While both estimators are unbiased, and apart from the small difference just mentioned, they seem to have similar variance, they are quite different in some other aspects. In particular, we may observe that the first estimator takes values in $[0,\infty)$, while the second estimator takes on values in $(-\infty,1]$. As we shall see, this will have a large impact on how useful these estimators are when used in Exp3.
Probability computation
Let $\hat S_{ti}$ stand for the the total estimated reward by the end of round $t$:
\begin{align*}
\hat S_{ti} \doteq \sum_{s=1}^{t} \hat{X}_{si}\,.
\end{align*}
A natural idea to set the action-selection probabilities $(P_{ti})_i$ so that actions with higher total estimated reward $\hat S_{ti}$ receive larger probabilities. While there are many ways to turn $\hat S_{ti}$ into probabilities, one particularly simple and popular way is to use an exponential weighting scheme. The advantage of this scheme is that it allows the algorithm to quickly increase the probability of outstanding actions, while quickly reducing the probability of poor ones. This may be especially beneficial if the action-set is large.
The formula that follows the above idea is to set
\begin{align}
P_{ti} \doteq \frac{\exp(\eta \hat S_{t-1,i}) }{\sum_j \exp( \eta \hat S_{t-1,j} ) } \,.
\label{eq:exp3update}
\end{align}
Here $\eta>0$ is a tuning parameter that controls how aggressively $P_{ti}$ is pushed towards the “one-hot distribution” that concentrates on the action whose estimated total reward is the largest: As $\eta\to\infty$, the probability mass in $P_{t,\cdot}$ quickly concentrates on $\argmax_i \hat S_{t-1,i}$. While there are many schemes for setting the value of $\eta$, in this post, for the sake of simplicity, we will consider the simplest setting where $\eta$ is set based on the problem’s major parameters, such as $K$ and $n$. What we will learn about setting $\eta$ can then be generalized, for example, to the setting when $n$, the number of rounds, is not known in advance.
For practical implementations, and also for the proof that comes, it is useful to note that the action-selection probabilities can also be updated in an incremental fashion:
\begin{align}
P_{t+1,i} = \frac{P_{ti} \exp(\eta \hat X_{ti})}{\sum_j P_{tj} \exp(\eta \hat X_{tj})}\,.
\label{eq:probupdate}
\end{align}
The Exp3 algorithm is a bit tricky to implement in a numerically stable manner when the number of rounds and $K$ are both large: In particular, the normalizing term above requires care when there are many orders of magnitude differences between the smallest and the larges probabilities. An easy way to avoid numerical instability is to incrementally calculate $\tilde S_{ti} = \hat S_{ti} – \min_j \hat S_{tj}$ and then use that $P_{t+1,i} = \exp(\eta \tilde S_{ti})/\sum_j \exp(\eta \tilde S_{tj} )$, where again one needs to be careful when calculating $\sum_j \exp(\eta \tilde S_{tj} )$.
To summarize, Exp3 (exponential weights for exploration and exploitation), uses either the reward estimates based on $\eqref{eq:impestimate}$ or the estimates based on $\eqref{eq:lossestimate}$ to estimate the rewards in every round. Then, the reward estimates are used to update the action selection probabilities using the exponential weighting scheme given by $\eqref{eq:probupdate}$. Commonly, the probabilities $P_{1i}$ are initialized uniformly, though the algorithm and the theory can also work with non-uniform initializations, which can be beneficial to express prior beliefs.
The expected regret of Exp3
In this section we will analyze the expected regret of Exp3. In all theorem statements here, Exp3 is assumed to be initialized with the uniform distribution, and it is assumed that Exp3 uses the “loss-based” reward estimates given by $\eqref{eq:lossestimate}$.
Our first result is as follows:
Theorem (Expected regret of Exp3):
For an arbitrary assignment $(x_{ti})_{ti}\in [0,1]^{nK}$ of rewards, the expected regret of Exp3 as described above and when $\eta$ is appropriately selected, satisfies
\begin{align*}
R_n \le 2 \sqrt{ n K \log(K) }\,.
\end{align*}
This, together with the previous result shows that up to a $\sqrt{\log(K)}$ factor, Exp3 achieves the minimax regret $R_n^*$.
Proof: Notice that it suffices to bound $R_{n,i} = \sum_{t=1}^n x_{ti} – \EE{ \sum_{t=1}^n X_t }$, the regret relative to action $i$ being used in all the rounds.
By the unbiasedness property of $\hat X_{ti}$, $\EE{ \hat S_{ni} } = \sum_{t=1}^n x_{ti}$. Also, $\Et{X_t} = \sum_i P_{ti} x_{ti} = \sum_i P_{ti} \Et{\hat X_{ti} }$ and thus $\EE{ \sum_{t=1}^n X_t } = \EE{ \sum_{t,i} P_{ti} \hat X_{ti} }$. Thus, defining $\hat S_n = \sum_{t,i} P_{ti} \hat X_{ti}$, we see that it suffices to bound the expectation of
\begin{align*}
\hat S_{ni} – \hat S_n\,.
\end{align*}
For this, we develop a bound on the exponentiated difference $\exp(\eta(\hat S_{ni} – \hat S_n))$. As we will see this is rather easy to bound. We start with bounding $\exp(\eta\hat S_{ni})$. First note that when $i$ is the index of the best arm, we won’t lose much by bounding this with $W_n \doteq \sum_{j} \exp(\eta(\hat S_{nj}))$. Define $\hat S_{0i} = 0$, so that $W_0 = K$. Then,
\begin{align*}
\exp(\eta \hat S_{ni} ) \le \sum_{j} \exp(\eta(\hat S_{nj})) = W_n = W_0 \frac{W_1}{W_0} \dots \frac{W_n}{W_{n-1}}\,.
\end{align*}
Thus, we need to study $\frac{W_t}{W_{t-1}}$:
\begin{align*}
\frac{W_t}{W_{t-1}} = \sum_j \frac{\exp(\eta \hat S_{t-1,j} )}{W_{t-1}} \exp(\eta \hat X_{tj} )
= \sum_j P_{tj} \exp(\eta \hat X_{tj} )\,.
\end{align*}
Now, since $\exp(x) \le 1 + x + x^2$ holds for any $x\le 1$ and $\hat X_{tj}$ by its construction is always below one (this is where we use for the first time that $\hat X_{tj}$ is defined by $\eqref{eq:lossestimate}$ and not by $\eqref{eq:impestimate}$), we get
\begin{align*}
\frac{W_t}{W_{t-1}} \le 1 + \eta \sum_j P_{tj} \hat X_{tj} + \eta^2 \sum_j P_{tj} \hat X_{tj}^2
\le \exp( \eta \sum_j P_{tj} \hat X_{tj} + \eta^2 \sum_j P_{tj} \hat X_{tj}^2 )\,,
\end{align*}
where we also used that $1+x \le \exp(x)$ which holds for any $x\in\R$. Putting the inequalities together we get
\begin{align*}
\exp( \eta \hat S_{ni} ) \le K \exp( \eta \hat S_n + \eta^2 \sum_{t,j} P_{tj} \hat X_{tj}^2 )\,.
\end{align*}
Taking the logarithm of both sides, dividing by $\eta>0$, and reordering gives
\begin{align}
\hat S_{ni} – \hat S_n \le \frac{\log(K)}{\eta} + \eta \sum_{t,j} P_{tj} \hat X_{tj}^2\,.
\label{eq:exp3core}
\end{align}
As noted earlier, the expectation of the left-hand side is $R_{ni}$, the regret against action $i.$ Thus, it remains to bound the expectation of $\sum_{t,j} P_{tj} \hat X_{tj}^2$. A somewhat lengthy calculation shows that $\Et{\sum_j P_{tj} \hat X_{tj}^2 } = \sum_j p_{tj}(1-2y_{tj}) + \sum_j y_{tj}^2 \le K$, where recall that $y_{tj} = 1-x_{tj}$ is the round $t$ “loss” of action $j$.
Hence,
\begin{align*}
R_{ni} \le \frac{\log(K)}{\eta} + \eta n K\,.
\end{align*}
Choosing $\eta = \sqrt{\log(K)/(nK)}$ gives the desired result.
QED
The heart of the proof is the use of the inequalities $\exp(x)\le 1 + x + x^2$ (true for $x\le 1$), followed by using $1+x\le \exp(x)$. We will now show an improved bound, which will have some additional benefits, as well. The idea is to replace the upper bound on $\exp(x)$ by
\begin{align}
\exp(x) \le 1 + x + \frac12 x^2\,,
\label{eq:expxupperbound}
\end{align}
which holds for $x\le 0$. The mentioned upper and lower bounds on $\exp(x)$ are shown on the figure below. From the figure, it is quite obvious that the second approximation is a great improvement over the first one when $x\le 0$. In fact, the second approximation is exactly the first two-terms of the Taylor series expansion of $\exp(x)$ and it is the best second order approximation of $\exp(x)$ at $x=0$.
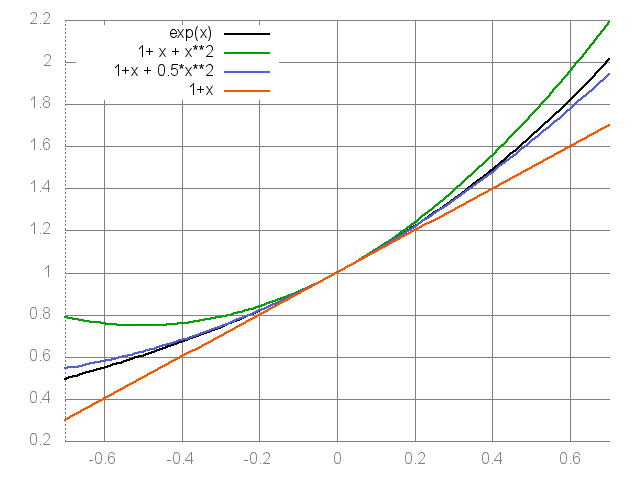
Various approximations to the exponential function.
Let us now put $\eqref{eq:expxupperbound}$ to a good use in proving a the tighter upper bound on the expected regret. By construction $\hat X_{tj}\le 1$, we compute
\begin{align*}
\exp(\eta \hat X_{tj} ) = \exp(\eta) \exp( \eta (\hat X_{tj}-1) )
\le \exp(\eta) \left\{1+ \eta (\hat X_{tj}-1) + \frac{\eta^2}{2} (\hat X_{tj}-1)^2\right\}\,,
\end{align*}
and thus, with more algebra and using $1+x\le \exp(x)$ again we get,
\begin{align*}
\sum_j P_{tj} \exp(\eta \hat X_{tj} )
&\le
%\exp(\eta) \sum_j P_{tj} \left(1+ \eta (\hat X_{tj}-1) + \frac{\eta^2}{2} (\hat X_{tj}-1)^2\right) \\
%&\le
%\exp(\eta) \left\{
%1+ \eta \sum_j P_{tj} (\hat X_{tj}-1) + \frac{\eta^2}{2} \sum_j P_{tj} (\hat X_{tj}-1)^2)
%\right\} \\
%&=
%\exp(\eta)\exp
%\left( \eta \sum_j P_{tj} (\hat X_{tj}-1) + \frac{\eta^2}{2} \sum_j P_{tj}(\hat X_{tj}-1)^2\right)\\
%&=
\exp\left( \eta \sum_j P_{tj} \hat X_{tj} + \frac{\eta^2}{2} \sum_j P_{tj}(\hat X_{tj}-1)^2\right)\,.
\end{align*}
We see that here we need to bound $\sum_j P_{tj} (\hat X_{tj}-1)^2$. To save on writing, it will be beneficial to switch to $\hat Y_{tj} = 1-\hat X_{tj}$ ($j\in [K]$), the estimates of the losses $y_{tj} = 1-x_{tj}$, $j\in [K]$. As done before, we also introduce $A_{tj} = \one{A_t=j}$ so that $\hat Y_{tj} = \frac{A_{tj}}{P_{tj}} y_{tj}$. Thus, $P_{tj} (\hat X_{tj}-1)^2 = P_{tj} \hat Y_{tj} \hat Y_{tj}$ and also $P_{tj} \hat Y_{tj} = A_{tj} y_{tj}\le 1$. Therefore, using that $\hat Y_{tj}\ge 0$, we find that $P_{tj} (\hat X_{tj}-1)^2 \le \hat Y_{tj}$.
This shows a second advantage of using $\eqref{eq:expxupperbound}$: When we use this inequality, the “second moment term” $\sum_j P_{tj} (\hat X_{tj}-1)^2$ can be seen to be bounded by $K$ in expectation (thanks to $\E_t[\hat Y_{tj}]\le 1$). Finishing as before, we get
\begin{align}
\hat S_{ni} – \hat S_n \le \frac{\log(K)}{\eta} + \frac{\eta}{2} \sum_{t,j} \hat Y_{tj}\,.
\label{eq:hpstartingpoint}
\end{align}
Now upper bounding $\sum_{t,j} \hat Y_{tj}$ by $nK$ and then taking expectations of both sides, followed by choosing $\eta$ to minimize the resulting right-hand side, we derive
\begin{align*}
R_n \le \sqrt{ 2 n K \log(K) }\,.
\end{align*}
In summary, the following improved result also holds:
Theorem (Improved upper bound on the expected regret of Exp3): For an arbitrary assignment $(x_{ti})_{ti}\in [0,1]^{nK}$ of rewards, the expected regret of Exp3 satisfies
\begin{align*}
R_n \le \sqrt{ 2 n K \log(K) }\,.
\end{align*}
The difference between this and our previous result is $\sqrt{2} = 1.4142\dots$, which shaves off approximately 30 percent of the previous bound!
High-probability bound on the regret: Exp3-IX
While it is reassuring that the expected regret of Exp3 on an adversarial problem is of the same size as the worst-case expected regret on stochastic bandit problems with bounded rewards, however, does this also mean that the random regret
\begin{align*}
\hat R_n = \max_i \sum_{t=1}^n x_{t,i} – \sum_{t=1}^n X_{t}\,,
\end{align*}
experienced in a single run will be small? While no such guarantee can be given (in the worst case $\hat R_n=n$ can easily hold — for some very bad sequence of outcomes), at least we would expect that the random regret is small with high probability. (In fact, we should have asked the same question for UCB and the other algorithms developed for the stochastic setting, a problem we may return to later.)
Before “jumping” into discussing the details of how such a high-probability bound can be derived, let us discuss the type of the results we expect to see. Looking at the regret definition, we may notice that the first term is deterministic, while the second is the sum of $n$ random variables each lying in $[0,1]$. If these were independent of each other, they would be subgaussian, thus the sum would also be subgaussian and we would expect to see a “small” tail. Hence, we may perhaps expect that the tail of $\hat R_n$ is also subgaussian? The complication is that the random variables in the sequence $(X_t)_t$ are far from being independent, but in fact are highly “correlated”. Indeed, $X_t = x_{t,A_t}$, where $A_t$ depends on all the previous $X_1,\dots,X_{t-1}$ in some complicated manner.
As it happens, the mentioned correlations can and will often destroy the thin tail property of the regret of the vanilla Exp3 algorithm that was described above. To understand why this happens note that the magnitude of the fluctuations of the sum $\sum_t U_t$ of independent random variables $U_t$ is governed by $\Var(\sum_t U_t)= \sum_t \Var(U_t)$. While $(\hat X_{ti})_s$ is not an independent sequence, the size of $\sum_t \hat X_{ti}$ is also governed by a similar quantity, the sum of predictable variations, $\sum_t \Vt{\hat X_{ti}}$. As noted earlier, for both estimators considered so far the conditional variance in round $t$ is $\Vt{\hat X_{ti}}\sim 1/P_{ti}$, hence we expect the reward estimates to have high fluctuations when $P_{ti}$ gets small. As written, nothing in the algorithm prevents this (see here). If the reward estimates fluctuate wildly, so will the probabilities $(P_{ti})_{ti}$, which means that perhaps the random regret $\hat R_n$ will also be highly varying. How can this be avoided? One idea is to change the algorithm to make sure that $P_{ti}$ is never too small: This can be done by mixing $(P_{ti})_i$ with the uniform distribution (pulling $(P_{ti})_i$ towards the uniform distribution). Shifting $(P_{ti})_i$ towards the uniform distribution increases the randomness of the actions and as such it can be seen as an explicit way of “forcing exploration”. Another option, which we will explore here, and which leads to a better algorithm, is to change the reward estimates to control their predictable variations. (In fact, forcing a certain amount of exploration alone is still insufficient to tame the large variations in the regret.)
Before considering how the reward estimates should be changed, it will be worthwhile to summarize what we know of the behavior of the random regret of Exp3. For doing this, we will switch to “losses” as this will remove some clutter in some formulae later. We start by rewriting inequality $\eqref{eq:hpstartingpoint}$ (which holds regardless of how the reward/loss estimates are constructed!) in terms of losses:
\begin{align*}
\hat L_n – \hat L_{ni} \le \frac{\log(K)}{\eta} + \frac{\eta}{2} \sum_{j} \hat L_{nj}\,.
\end{align*}
Here, $ L_n$ and $\hat L_{ni}$ re defined by
\begin{align*}
\hat L_n = \sum_{t=1}^n \sum_{j=1}^K P_{t,j} \hat Y_{tj}\, \quad \text{ and }\,\quad
\hat L_{ni} = \sum_{t=1}^n \hat Y_{ti}\,
\end{align*}
where as usual $\hat Y_{tj} = 1-\hat X_{tj}$. Now, defining
\begin{align*}
\tilde L_n = \sum_{t=1}^n \hat y_{t,A_t}\, \quad\text{ and }\,\quad
L_{ni} = \sum_{t=1}^n y_{ti}
\end{align*}
(recall that $y_{tj} = 1-x_{tj}$), the random regret $\hat R_{ni} = \sum_{t=1}^n x_{ti} – \sum_{t=1}^n X_t$ against the $i$th expert becomes $\tilde L_n – L_{ni}$, and thus,
\begin{align}
\hat R_{ni}
& = \tilde L_n – L_{ni}
= (\tilde L_n – \hat L_n) + (\hat L_n – \hat L_{ni}) + (\hat L_{ni} – L_{ni}) \nonumber \\
& \le \frac{\log(K)}{\eta} + \frac{\eta}{2}\, \sum_{j} L_{nj}\,\, +
(\tilde L_n – \hat L_n) + (\hat L_{ni} – L_{ni})
+ \frac{\eta}{2}\, \sum_j (\hat L_{nj}-L_{nj}) \,.
\label{eq:mainexp3ix}
\end{align}
Thus, to bound the random regret all we have to do is to bound $\tilde L_n – \hat L_n$ and the terms $\hat L_{nj}-L_{nj}$.
To do this, we we will need the modified reward estimates. Recalling that the goal was to control the estimate’s variance, and the large variance of $\hat X_{ti}$ was the result of dividing by a potentially small $P_{ti}$, a simple “fix” is to use
\begin{align*}
\hat X_{ti} = 1-\frac{\one{A_t=i}}{P_{ti}+\gamma} \, (1-X_t)\,,
\end{align*}
or, when using losses,
\begin{align*}
\hat Y_{ti} = \frac{\one{A_t=i}}{P_{ti}+\gamma} \, Y_t\,.
\end{align*}
Here $\gamma\ge 0$ is a small constant whose value, as usual, will be chosen later. When these estimates are used in the standard “exponential update” (cf. $\eqref{eq:probupdate}$) we get an algorithm called Exp3-IX. Here, suffix IX refers to that the estimator makes the algorithm explore in an implicit fashion, as will be explained next.
Since a larger value is used in the denominator, for $\gamma>0$, $\hat Y_{ti}$ is biased. In particular, the bias in $\hat Y_{ti}$ is “downwards”, i.e., $\Et{\hat Y_{ti}}$ will be a lower bound on $y_{ti}$. Symmetrically, the value of $\hat X_{ti}$ is inflated. In other words, the estimator will be optimistically biased. But will optimism will help? And did anyone say optimism is for fools? Anyhow, the previous story repeats: optimism facilitates exploration. In particular, as the estimates are optimistic, the probabilities in general will be pushed up. The effect is the largest for the smallest probabilities, thus increasing “exploration” in an implicit fashion. Hence the suffix “IX”.
Let us now return to developing a bound on the random regret. Thanks to the optimistic bias of the new estimator, we expect $\hat L_{ni}-L_{ni}$ to be negative. This is quite helpful given that this term appears multiple times in $\eqref{eq:mainexp3ix}$! But how about $\tilde L_n – \hat L_n$? Writing $Y_t = \sum_j A_{tj} y_{tj}$, we calculate
\begin{align*}
Y_t – \sum_j P_{tj} \hat Y_{tj}
& = \sum_j \left(1 – \frac{P_{tj}}{P_{tj}+\gamma} \right) \, A_{t,j} y_{t,j}
= \gamma \sum_j \frac{A_{t,j}}{P_{tj}+\gamma} y_{t,j} = \gamma \sum_j \hat Y_{tj}\,.
\end{align*}
Therefore, $\tilde L_n – \hat L_n = \gamma \sum_j \hat L_{nj} = \gamma \sum_j L_{nj} + (\hat L_{nj}-L_{nj})$. Hmm, $\hat L_{nj}-L_{nj}$ again! Plugging the expression developed into $\eqref{eq:mainexp3ix}$, we get
\begin{align}
\hat R_{ni}
& \le \frac{\log(K)}{\eta}
+ \left(\gamma+\frac{\eta}{2}\right)\, \sum_{j} L_{nj}\,\, + (\hat L_{ni} – L_{ni})
+ \left(\gamma+\frac{\eta}{2}\right)\, \sum_j (\hat L_{nj}-L_{nj}) \\
& \le \frac{\log(K)}{\eta}
+ \left(\gamma+\frac{\eta}{2}\right) nK \,\, + (\hat L_{ni} – L_{ni})
+ \left(\gamma+\frac{\eta}{2}\right)\, \sum_j (\hat L_{nj}-L_{nj}) \,. \label{eq:exp3hp3}
\end{align}
The plan to bound $\hat L_{ni} – L_{ni}$ is to use an adaptation of Chernoff’s method, which we discussed earlier for bounding the tails of subgaussian random variables $X$. In particular, according to Chernoff’s method, $\Prob{X>\epsilon}\le \EE{\exp(X)} \exp(-\epsilon)$ and so to bound the tail of $X$ it suffices to bound $\EE{\exp(X)}$. Considering that $\exp(\hat L_{ni} – L_{ni}) = \prod_{t=1}^n M_{ti}$ where $M_{ti}=\exp( \hat Y_{ti}-y_{ti})$, we see that the key is to understand the magnitude of the conditional expectations of the terms $\exp( \hat Y_{ti}) = \exp(\frac{A_{ti}y_{ti}}{P_{ti}+\gamma})$. As usual, we aim to use a polynomial upper bound. In this case, we consider a linear upper bound:
Lemma: For any $0\le x \le 2\lambda$,
\begin{align*}
\exp( \frac{x}{1+\lambda} ) \le 1 + x\,.
\end{align*}
Note that $1+x\le \exp(x)$. What the lemma shows is that by slightly discounting the argument of the exponential function, in a bounded neighborhood of zero, $1+x$ can be an upper bound, or, equivalently, slightly inflating the linear term in $1+x$, the linear lower bound becomes an upper bound.
Proof: We rely on two well-known inequalities. The first inequality is $\frac{2u}{1+u} \le \log(1+ 2u)$ which holds for $u\ge 0$ (note that as $u\to 0+$, the inequality becomes tight). Thanks to this inequality,
\begin{align*}
\frac{x}{1+\lambda}
= \frac{x}{2\lambda} \, \frac{2\lambda}{1+\lambda}
\le \frac{x}{2\lambda} \, \log(1+2\lambda)
\le \log\left( 1+ 2 \lambda \frac{x}{2\lambda} \right) = \log(1+x)\,,
\end{align*}
where the second inequality uses $x \log(1+y) \le \log(1+xy)$, which holds for any $x\in [0,1]$ and $y>-1$.
QED.
Based on this, we are ready to prove the following result, which shows that the upper tail of a negatively biased sum is small. The result is tweaked so that it can save us some constant factors later:
Lemma (Upper tail of negatively biased sums): Let $(\cF_t)_{1\le t \le n}$ be a filtration and for $i\in [K]$ let $(\tilde Y_{ti})_t$ be $(\cF_t)_t$-adapted (i.e., for each $t$, $\tilde Y_{ti}$ is $\cF_t$-measurable) such that for
any $S\subset[K]$ with $|S|>1$, $\E_{t-1}\left[\prod_{i\in S} \tilde Y_{ti} \right] \le 0$, while for any $i\in [K]$, $\E_{t-1}[\tilde Y_{ti}]= y_{ti}$.
Further, let $(\alpha_{ti})_{ti}$, $(\lambda_{ti})_{ti}$ be real-valued predictable random sequences (i.e., $\alpha_{ti}$ and $\lambda_{ti}$ are $\cF_{t-1}$-measurable). Assume further that for all $t,i$, $0\le \alpha_{ti} \tilde Y_{ti} \le 2\lambda_{ti}$. Then, for any $0\le \delta \le 1$, with probability at least $1-\delta$,
\begin{align*}
\sum_{t,i} \alpha_{ti} \left( \frac{\tilde Y_{ti}}{1+\lambda_{ti}} – y_{ti} \right) \le \log\left( \frac1\delta \right)\,.
\end{align*}
The proof, which is postponed to the end of the post, just combines Chernoff’s method and the previous lemma as suggested above. Equipped with this result, we can easily bound the terms $\hat L_{ni}-L_{ni}$:
Lemma (Loss estimate tail upper bound):
Fix $0\le \delta \le 1$. Then the probability that the inequalities
\begin{align}
\max_i \hat L_{ni} – L_{ni} \le \frac{\log(\frac{K+1}{\delta})}{2\gamma}\,, \qquad \text{and} \qquad
\sum_i (\hat L_{ni} – L_{ni}) \le \frac{\log(\frac{K+1}{\delta}) }{2\gamma}\,
\label{eq:losstailbounds}
\end{align}
both hold is at least $1-\delta$.
Proof: Fix $0\le \delta’ \le 1$ to be chosen later. We have
\begin{align*}
\sum_i (\hat L_{ni} – L_{ni} )
& = \sum_{ti} \frac{A_{ti}y_{ti}}{ P_{ti}+\gamma } – y_{ti}
= \frac{1}{2\gamma} \,
\sum_{ti} 2\gamma \left( \frac{1}{1+\frac{\gamma}{P_{ti}}}\frac{A_{ti} y_{ti}}{ P_{ti} } – y_{ti}\right)\,.
\end{align*}
Introduce $\lambda_{ti} = \frac{\gamma}{P_{ti}}$, $\tilde Y_{ti} = \frac{A_{ti} y_{ti}}{ P_{ti} }$ and $\alpha_{ti} = 2\gamma$. It is not hard to see then that the conditions of the previous lemma are satisfied (in particular, for $S\subset [K]$ if $i,j\in S$ and $i\ne j$ then
$\tilde Y_{ti} \tilde Y_{tj}= 0$ thanks to that for $i\ne j$, $A_{ti}A_{tj}=0$ holds), while $\E_{t-1}[\tilde Y_{ti}]=y_{ti}$. Therefore, outside of an event $\cE_0$ that has a probability of at most $\delta’$,
\begin{align}\label{eq:sumbound}
\sum_i (\hat L_{ni} – L_{ni} ) \le \frac{\log(1/\delta’)}{2\gamma}.
\end{align}
Similarly, we get that for any fixed $i$, outside of an event of probability $\cE_i$ that has a probability of at most $\delta’$,
\begin{align}
\hat L_{ni} – L_{ni}\le \frac{\log(1/\delta’)}{2\gamma}\,.
\label{eq:indbound}
\end{align}
To see this latter just use the previous argument but now set $\alpha_{tj}=\one{j=i} 2\gamma$. Thus, outside of the event, $\cE =\cE_0 \cup \cE_1 \cup \dots \cup \cE_K$, all of $\eqref{eq:sumbound}$ and $\eqref{eq:indbound}$ hold (the latter for all $i$). The total probability of $\cE$ is $\Prob{\cE}\le \sum_{i=0}^K \Prob{\cE_i}\le (K+1)\delta’$. Choosing $\delta’ = \delta/(K+1)$ gives the result.
QED.
Putting everything together, we get the main result of this section:
Theorem (High-probability regret of Exp3-IX):
Let $\hat R_n$ be the random regret of Exp3-IX run with $\gamma = \eta/2$. Then, choosing $\eta = \sqrt{\frac{2\log(K+1)}{nK}}$, for any $0\le \delta \le 1$, the inequality
\begin{align}
\label{eq:exp3unifhp}
\hat R_n \le \sqrt{8.5 nK\log(K+1)} +\left(\sqrt{ \frac{nK}{2\log(K+1)} } +1\right)\,
\log(1/\delta)\,
\end{align}
hold with probability at least $1-\delta$. Further, for any $0\le \delta \le 1$, if $\eta = \sqrt{\frac{\log(K)+\log(\frac{K+1}{\delta})}{nK}}$, then
\begin{align}
\label{eq:exp3deltadephp}
\hat R_{n}
\le 2 \sqrt{ (2\log(K+1) + \log(1/\delta) ) nK } + \log\left(\frac{K+1}{\delta}\right)
\end{align}
holds with probability at least $1-\delta$.
Note that the choice of $\eta$ and $\gamma$ that leads to $\eqref{eq:exp3unifhp}$ is independent of $\delta$, while the choice that leads to $\eqref{eq:exp3deltadephp}$ depends on the value of $\delta$. As expected, the second bound is tighter.
Proof: Introduce $B = \log( \frac{K+1}{\delta} )$. Consider the event when $\eqref{eq:losstailbounds}$ holds. On this event, thanks to $\eqref{eq:exp3hp3}$, simultaneously, for all $i\in [K]$,
\begin{align*}
\hat R_{ni}
& \le \frac{\log(K)}{\eta}
+ \left(\gamma+\frac{\eta}{2}\right) nK
+ \left(\gamma+\frac{\eta}{2}+1\right)\, \frac{B}{2\gamma}.
%\label{eq:exp3ixhp4}
\end{align*}
Choose $\gamma=\eta/2$ and note that $\hat R_n = \max R_{ni}$. Hence, $\hat R_{n} \le \frac{\log(K)+B}{\eta} + \eta\, nK + B$. Choosing $\eta = \sqrt{\frac{\log(K)+B}{nK}}$, we get
\begin{align*}
\hat R_{n} & \le 2 \sqrt{ (\log(K)+B) nK } + B
\le 2 \sqrt{ (2\log(K+1) + \log(1/\delta) ) nK } + \log(\frac{K+1}{\delta})\,,
\end{align*}
while choosing $\eta = \sqrt{\frac{2\log(K+1)}{nK}}$, we get
\begin{align*}
\hat R_{n}
& \le (2\log(K+1)+\log(1/\delta)) \sqrt{ \frac{nK}{2\log(K+1)} }
+ \sqrt{ \frac{2\log(K+1)}{nK} }\, nK + \log(\frac{K+1}{\delta}) \\
& = 2\sqrt{2nK\log(K+1)} +\left(\sqrt{ \frac{nK}{2\log(K+1)} } +1\right)\,
\log(\frac{K+1}{\delta})\,.
\end{align*}
By the previous lemma, the event when $\eqref{eq:losstailbounds}$ holds has a probability of at least $1-\delta$, thus finishing the proof.
QED.
It is apparent from the proof that the bound can be slightly improved by choosing $\eta$ and $\gamma$ to optimize the upper bounds. A more pressing issue though is that the choice of these parameters is tied to the number of rounds. Our earlier comments apply: The result can be re-proved for decreasing sequences $(\eta_t)$, $(\gamma_t)$, and by appropriately selecting these we can derive a bound which is only slightly worse than the one presented here. An upper bound on the expected regret of Exp3-IX can be easily obtained by “tail integration” (i.e., by using that for $X\ge 0$, $\E{X} = \int_0^\infty \Prob{X>x} dx$). The upper bound that can be derived this way is only slightly larger than that derived for Exp3. In practice, Exp3-IX is highly competitive and is expected to be almost always better than Exp3.
Summary
In this post we introduced the adversarial bandit model as a way of deriving guarantees that do not depend on the specifics of how the rewards observed are generated. In particular, the only assumption made was that the rewards belong to a known bounded range. As before, performance is quantified as the loss due to missing to choose the action that has the highest total reward. As expected, algorithms developed for the adversarial model, will also “deliver” in the stochastic bandit model. In fact, the avdersarial minimax regret is lower bounded by the minimax regret of stochastic problems, which resulted in a lower bound of $\Omega(\sqrt{nK})$. The expected regret of Exp3, an algorithm which combines reward estimation and exponential weighting, was seen to match this up to a $\sqrt{\log K}$ factor. We discussed multiple variations of Exp3, comparing benefits and pitfalls of using various reward estimates. In particular, we discussed Exp3-IX, a variant that uses optimistic estimates for the rewards. The primary benefit of using optimistic estimates is a better control of the variance of the reward estimates and as a result Exp3-IX has a better control of the upper tail of the random regret.
This post, however, only scratched the surface of all the research that is happening on adversarial bandits. In the next post we will consider Exp4, which builds on the ideas presented here, but addresses a more challenging a practical problem. In addition we also hope to discuss lower bounds on the high probability regret, which we have omitted so far.
The remaining proof
Here we prove the lemma on the upper tail of negatively biased sums.
Proof: Let $\Et{\cdot}$ be the conditional expectation with respect to $\cF_t$: $\Et{U}\doteq \EE{U|\cF_t}$. Thanks to $\exp(x/(1+\lambda))\le 1+x$ which was shown to hold for $0\le x \le 2\lambda$ and the assumptions that $0\le \alpha_{ti} \tilde Y_{ti} \le 2\lambda_{ti}$, we have
\begin{align}
\E_{t-1} \, \exp\left(\sum_i \frac{\alpha_{ti} \tilde Y_{ti}}{1+\lambda_{ti}} \right)
& \le \E_{t-1} \prod_i (1+\alpha_{ti} \tilde Y_{ti})\nonumber \\
& \le 1+\E_{t-1} \sum_i \alpha_{ti} \tilde Y_{ti}\nonumber \\
& = 1+ \sum_i \alpha_{ti} y_{ti} \nonumber \\
& \le \exp(\sum_i \alpha_{ti} y_{ti})\,.
\label{eq:basicexpineq}
\end{align}
Here, the second inequality follows from the assumption that for $S\subset [K]$ with $|S|>1$, $\E_{t-1} \prod_{i\in S}\tilde Y_{ti} \le 0$, the third one follows from the assumption that $\E_{t-1} \tilde Y_{ti} = y_{ti}$, while the last one follows from $1+x\le \exp(x)$.
Define
\begin{align*}
Z_t = \exp\left( \sum_i \alpha_{ti} \left(\frac{\tilde Y_{ti}}{1+\lambda_{ti}}-y_{ti}\right) \right)\,
\end{align*}
and let $M_t = Z_1 \dots Z_t$, $t\in [n]$ with $M_0 = 1$. By $\eqref{eq:basicexpineq}$,
$\E_{t-1}[Z_t]\le 1$. Therefore,
\begin{align*}
\E[M_t] = \E[ \E_{t-1}[M_t] ] = \E[ M_{t-1} \E_{t-1}[Z_t] ] \le \E[ M_{t-1} ] \le \dots \le \E[ M_0 ] =1\,.
\end{align*}
Applying this with $t=n$, we get
$\Prob{ \log(M_n) \ge \log(1/\delta) } =\Prob{ M_n \delta \ge 1} \le \EE{M_n} \delta \le \delta$.
QED.
References
The main reference, which introduced Exp3 (and some variations of it) is by Peter Auer, Nicolò Cesa-Bianchi, Yoav Freund and Robert E. Schapire:
- Peter Auer, Nicolò Cesa-Bianchi, Yoav Freund, Robert E. Schapire: The Nonstochastic Multiarmed Bandit Problem. SIAM Journal on Computing, Volume, 2003, pp. 48-77.
- The Exp3-IX algorithm is quite new and is due to Tomas Kocak, Gergely Neu, Mical Valko and Remi Munos. That paper actually focuses on a more complex version of the bandit problem rather than high probability bounds, which were given later by Gergely.
Notes
Note 1: There are many other ways that to relax the rigidity of stationary stochastic environments. Some alternatives, other than considering a fully adversarial setting include making mixing assumptions about the rewards, assuming hidden or visible states, or drifts just to mention a few. Drifts (nonstationarity) can and is studies in the adversarial setting, too.
Note 2: What happens when the range of the rewards is unknown? This has been studied e.g., by Allenberg et al. See: Allenberg, C., Auer, P., Gyorfi, L., and Ottucsak, Gy. (2006). Hannan consistency in on-line learning in case of unbounded losses under partial monitoring. In ALT, pages 229–243
Note 3: A perhaps even more basic problem than the one considered here is when the learner receives all $(x_{t,i})_i$ by the end of round $t$. This is sometimes called the full-information setting. The algorithm can simply fall back to just using exponential weighting with the total rewards. This is sometimes called the Hedge algorithm, or the “Exponential Weights Algorithm” (EWA). The underlying problem is sometimes called “prediction with expert advice”. The proof as written goes through, but one should replace the polynomial upper bound on $\exp(x)$ with Hoeffding’s lemma. This analysis gives a regret of $\sqrt{\frac{1}{2} n \log(K)}$, which is optimal in an asymptotic sense.
Note 4: As noted earlier, it is possible to remove the $\sqrt{\log(K)}$ factor from the upper bound on the expected regret. For details, see this paper by Sebastian Bubeck and Jean-Yves Audibert.
Note 5: By initializing $(P_{0i})_i$ to be biased towards some actions, the regret of Exp3 improves under the favorable environments when the “prior” guess is correct in that the action that $(P_{0i})_i$ is biased towards has a large total reward. However, this does not come for free, as shown in this paper by Tor.
Note 6: An alternative to the model considered is to let the environment choose $(x_{ti})$ based on the learner’s past actions. This is a harsher environment model. Nevertheless, the result we obtained can be generalized to this setting with no problems. It is another question whether in such “reactive” environments, the usual regret definition makes sense. Sometimes it does (when the environment arises as part of a “reduction”, i.e., it is made up by an algorithm itself operating in a bigger context). Sometimes the environments that do not react are called oblivious, while the reactive ones are said to be non-oblivious.
Note 7: A common misconception in connection to the adversarial framework is that it is a good fit for nonstationary environments. While the adversarial framework does not rule out nonstationary environments, the regret concept used has stationarity built into it and an algorithm that keeps the regret (as defined here) small will typically be unsuitable for real nonstationary environments, where conditions change or evolve. What happens in a truly nonstationary setting is that the single best action in hindsight will not collect much reward. Hence, the goal here should be to compete with the best action sequences computed in hindsight. A reasonable goal is to design algorithms which compete simultaneously with many action sequences of varying complexity and make the regret degrade in a graceful manner as the complexity of the competing action sequence increases (complexity can be measured by the number of action-switches over time).
Note 8: As noted before, regardless of which estimator is used to estimate the rewards, $\Vt{\hat X_{ti}} \sim 1/P_{ti}$. The problem then is that if $P_{ti}$ gets very very small, the predictable variance will be huge. It is instructive to think through whether and how $P_{ti}$ can take on very small values. Consider first the loss-based estimator given by $\eqref{eq:lossestimate}$. For this estimator, when $P_{t,A_t}$ and $X_t$ are both small, $\hat X_{t,A_t}$ can take on a large negative value. Through the update formula $\eqref{eq:exp3update}$ this then translates into $P_{t+1,A_t}$ being squashed aggressively towards zero. A similar issue arises with the reward-based estimator given by $\eqref{eq:impestimate}$. The difference is that now it will be a “positive surprise” ($P_{t,A_t}$ small, $X_t$ large) that pushes the probabilities towards zero. In fact, for such positive surprises, the probabilities of all actions but $A_t$ will be pushed towards zero. This means that in this version dangerously small probabilities can be expected to be seen even more frequently.
Note 9: The argument used in the last steps of proving the bound on the upper tail of the loss estimates had the following logic: Outside of $\cE_i$, some desired relation $R_i$ holds. If the probability of $\cE_i$ is bounded by $\delta$, then outside of $\cup_{i\in [m]} \cE_i$, all of $R_1,\dots, R_m$ hold true. Thus, with probability at least $1-m\delta$, $R_1,\dots, R_m$ are simultaneously true. This is called the “union bound argument”. In the future we will routinely use this argument without naming the error events $\cE_i$ and skipping the details.
Note 10: It was mentioned that the size of fluctuations of the sum of a sequence of $(\cF_t)_t$-adapted random variables is governed by the sum of predictable variations. This is best accounted for in the tail inequalities named after Bernstein and Freedman. The relevant paper of Freedman can be found here.



Thanks for your great work, really useful.
After equation (7) “An easy way to avoid numerical instability is to incrementally calculate $$\tilde S_{ti}=\hat S_{ti}–min_j \hat S_{ti}$$…” – should it not be $$\tilde S_{ti}=\hat S_{ti}–min_j \hat S_{tj}$$?
Yes, you are right! Thanks for the catch! I have updated the page.
Thanks, good catch. We have corrected the page.
I think the definition of \tilde L_n = \sum_{t=1}^n \hat Y_{t,A_t}\ seems wrong.
Maybe it might be corrected like this: \tilde L_n = \sum_{t=1}^n \ Y_{t}\
Hi! Thanks, good catch again. The correction indeed work and I have implemented it.
– Csaba
This is a question on Problem 18.5 from the book. The definition of regret seems to be wrong. Also, can you please check whether the regret bound is correct or not. In my understanding, it should be
\[\mathbb{E}[R_n] \leq \sqrt{2nkO^m\log(O)}.\]
Please correct me if I am wrong.
Hi Abhishek,
What is wrong with the definition? In the version of Thursday 27th June, 2019, the regret is defined as $R_n = \max_{\phi} \sum_{t=1}^m x_{t,\phi(o_t,\dots,o_{t-m})} – X_{t,A_t}$, which looks fine to me. Actually, the regret should be $\mathbb{E}[R_n] \leq \sqrt{2nk O^m \log(k)}$, so it was indeed incorrect in the exercise, but inside the $\log$ one should have $\log(k)$ and not $\log(O)$ (the number of $\phi$ maps is $k^{O^m}$). I’ll correct this in the next version of the book. Thanks for the catch.
Best,
Csaba
PS: Sorry for the late reply.